Trong thế giới ngày càng phát triển của Trí tuệ Nhân tạo (AI) và Machine Learning, hồi quy tuyến tính đóng một vai trò quan trọng như một công cụ phân tích và dự đoán mạnh mẽ. Đây là một trong những kỹ thuật học máy đầu tiên được phát triển và vẫn tiếp tục được sử dụng rộng rãi trong nhiều lĩnh vực ứng dụng khác nhau. Hồi quy tuyến tính cung cấp một cách tiếp cận đơn giản nhưng hiệu quả để khám phá mối quan hệ giữa các biến, cho phép chúng ta dự đoán giá trị của một biến dựa trên các biến khác.
Hồi quy tuyến tính
Hồi quy tuyến tính là một phương pháp thống kê được sử dụng để mô hình hóa mối quan hệ giữa một biến phụ thuộc (hay biến mục tiêu) và một hoặc nhiều biến độc lập (hay biến dự đoán). Mục đích chính của hồi quy tuyến tính là tìm ra một hàm tuyến tính, được gọi là hàm hồi quy, để mô tả mối liên hệ giữa các biến này một cách chính xác nhất có thể.
Phương trình hồi quy tuyến tính
Phương trình hồi quy tuyến tính có dạng như sau:
y = β0 + β1x1 + β2x2 + ... + βnxnTrong đó:
- y: Biến mục tiêu
- x1, x2, …, xn: Các biến dự đoán
- β0: Hệ số giao (intercept)
- β1, β2, …, βn: Các hệ số hồi quy (regression coefficients)
Mục tiêu của hồi quy tuyến tính là tìm ra các giá trị của các hệ số hồi quy (β0, β1, …, βn) sao cho hàm hồi quy xấp xỉ tốt nhất mối quan hệ giữa biến mục tiêu và các biến dự đoán. Quá trình này được gọi là “lắp mô hình” (model fitting) và sử dụng dữ liệu đào tạo để ước tính các hệ số.
Các loại hồi quy tuyến tính
Có hai loại chính của hồi quy tuyến tính:
- Hồi quy tuyến tính đơn biến: Trong trường hợp này, chỉ có một biến dự đoán duy nhất.
- Hồi quy tuyến tính đa biến: Trong trường hợp này, có nhiều hơn một biến dự đoán được sử dụng để dự đoán biến mục tiêu.
Giả định của hồi quy tuyến tính
Để đảm bảo rằng kết quả của hồi quy tuyến tính là chính xác và tin cậy, một số giả định cần được đáp ứng:
- Tuyến tính: Mối quan hệ giữa biến mục tiêu và các biến dự đoán ph là tuyến tính.
- Phân phối chuẩn: Các sai số (hay nhiễu) phải tuân theo phân phối chuẩn.
- Phương sai không đổi: Phương sai của sai số phải không đổi trên toàn bộ miền giá trị của các biến dự đoán.
- Không có đa cộng tuyến: Các biến dự đoán không được tương quan mạnh với nhau.
- Không có tự tương quan: Các sai số phải độc lập với nhau.
Hồi quy tuyến tính trong học máy
Trong bối cảnh Học máy, hồi quy tuyến tính được sử dụng rộng rãi cho các tác vụ dự đoán và phân tích dữ liệu. Nó cung cấp một phương pháp đơn giản nhưng hiệu quả để mô hình hóa mối quan hệ giữa các biến và cho phép dự đoán giá trị của một biến mục tiêu dựa trên các biến dự đoán.
Ưu điểm của hồi quy tuyến tính
- Đơn giản và dễ hiểu: Hồi quy tuyến tính có cấu trúc đơn giản và dễ hiểu, làm cho nó trở thành một lựa chọn phổ biến để bắt đầu với các bài toán phân tích dữ liệu.
- Hiệu suất tính toán tốt: Các thuật toán hồi quy tuyến tính có thể được tính toán một cách hiệu quả, đặc biệt với các tập dữ liệu lớn.
- Khả năng giải thích: Các hệ số hồi quy cung cấp một cách để đánh giá tầm quan trọng của các biến dự đoán và ảnh hưởng của chúng đối với biến mục tiêu.
- Không yêu cầu nhiều tiền xử lý dữ liệu: Hồi quy tuyến tính có thể được áp dụng trực tiếp cho dữ liệu thô mà không cần nhiều tiền xử lý.
Nhược điểm của hồi quy tuyến tính
- Giả định tuyến tính: Hồi quy tuyến tính giả định mối quan hệ giữa biến mục tiêu và các biến dự đoán là tuyến tính, điều này có thể không đúng trong nhiều trường hợp thực tế.
- Khó khăn với dữ liệu phức tạp: Hồi quy tuyến tính có thể gặp khó khăn khi xử lý dữ liệu phức tạp, như dữ liệu không tuyến tính hoặc có nhiều chiều.
- Nhạy cảm với dữ liệu bất thường: Hồi quy tuyến tính có thể bị ảnh hưởng bởi các điểm dữ liệu bất thường (outliers) và có thể dẫn đến kết quả không chính xác.
- Đa cộng tuyến: Khi các biến dự đoán tương quan cao với nhau, điều này có thể gây ra sự không ổn định trong ước tính các hệ số hồi quy.
Ứng dụng của hồi quy tuyến tính trong học máy
Hồi quy tuyến tính có nhiều ứng dụng quan trọc trong lĩnh vực Học máy, bao gồm:
Dự đoán giá nhà đất
Một trong những ứng dụng phổ biến của hồi quy tuyến tính trong Học máy là dự đoán giá nhà đất. Bằng cách sử dụng các biến đầu vào như diện tích, vị trí, số phòng ngủ, số phòng tắm, hồ bơi, v.v., mô hình hồi quy tuyến tính có thể dự đoán giá trị của một căn nhà dựa trên các yếu tố này. Điều này giúp người mua, người bán và các nhà đầu tư trong việc đưa ra quyết định thông minh về thị trường bất động sản.
Dự đoán doanh số bán hàng
Trong lĩnh vực kinh doanh, hồi quy tuyến tính được sử dụng để dự đoán doanh số bán hàng dựa trên các yếu tố như chi phí quảng cáo, mùa vụ, giá cả, v.v. Bằng cách xây dựng một mô hình hồi quy từ dữ liệu lịch sử, các doanh nghiệp có thể đưa ra dự đoán chính xác về doanh số bán hàng trong tương lai và điều chỉnh chiến lược kinh doanh của họ.
Phân loại dữ liệu
Ngoài việc dùng để dự đoán giá trị số, hồi quy tuyến tính cũng có thể được áp dụng trong các bài toán phân loại dữ liệu. Với việc thiết lập ngưỡng (threshold) cho biến mục tiêu, mô hình hồi quy tuyến tính có thể được sử dụng để phân loại dữ liệu thành các nhóm khác nhau. Ví dụ, trong bài toán phân loại khách hàng tiềm năng, mô hình hồi quy tuyến tính có thể được sử dụng để dự đoán xác suất một khách hàng sẽ mua sản phẩm dựa trên các yếu tố như tuổi, thu nhập, v.v.
Xác định ảnh hưởng của yếu tố
Hồi quy tuyến tính cũng được sử dụng để xác định mức độ ảnh hưởng của các yếu tố đến biến mục tiêu. Bằng cách kiểm tra hệ số hồi quy của mỗi biến độc lập, chúng ta có thể biết được mức độ ảnh hưởng tích cực hoặc tiêu cực của từng yếu tố đối với biến mục tiêu. Điều này giúp chúng ta hiểu rõ hơn về quan hệ giữa các biến và có thể đưa ra các quyết định chiến lược dựa trên thông tin này.
Các phương pháp hồi quy tuyến tính trong học máy
Trong Học máy, có nhiều phương pháp khác nhau để thực hiện hồi quy tuyến tính, bao gồm:
Hồi quy tuyến tính thông thường (Ordinary Least Squares – OLS)
Phương pháp OLS là phương pháp phổ biến nhất để ước lượng các hệ số hồi quy trong mô hình tuyến tính. Mục tiêu của OLS là tìm ra các hệ số sao cho tổng bình phương của sai số giữa giá trị dự đoán và giá trị quan sát là nhỏ nhất. Phương pháp này đòi hỏi giả định về phân phối chuẩn của sai số và không có đa cộng tuyến giữa các biến độc lập.

Hồi quy Ridge
Hồi quy Ridge là một phương pháp điều chỉnh trong đó một hạng stricness được áp dụng cho hệ số của các biến dự đoán. Phương pháp này giúp giảm overfitting trong trường hợp có đa cộng tuyến giữa các biến độc lập. Hồi quy Ridge thêm một thành phần điều chỉnh vào hàm mất mát để giảm giá trị tuyệt đối của các hệ số hồi quy.
Hồi quy Lasso
Hồi quy Lasso là một phương pháp khác để giảm overfitting trong mô hình hồi quy tuyến tính. Khác với Ridge, Hồi quy Lasso sử dụng norm chuẩn thứ nhất thay vì norm chuẩn thứ hai để điều chỉnh hệ số. Điều này có thể dẫn đến việc có một số hệ số bằng không, từ đó giúp trong việc chọn lọc biến độc lập quan trọng.
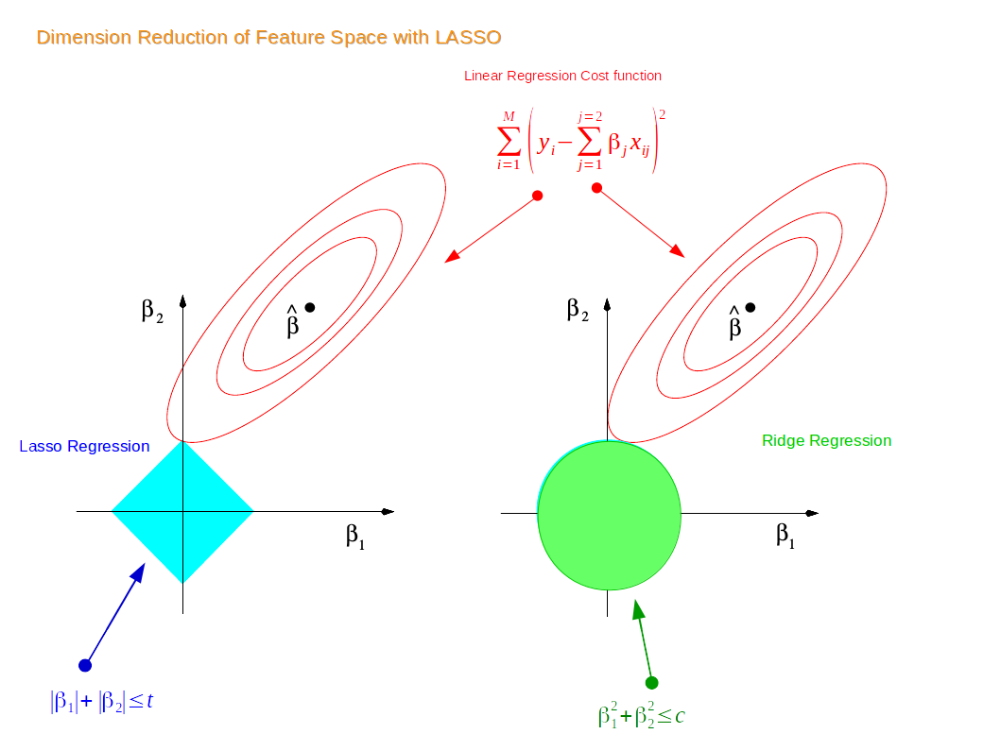
Elastic Net
Elastic Net kết hợp cả hai phương pháp Ridge và Lasso bằng cách thêm cả hai thành phần điều chỉnh vào hàm mất mát. Phương pháp này giúp giải quyết vấn đề đa cộng tuyến và chọn lọc biến độc lập quan trọng, đồng thời giảm overfitting trong mô hình hồi quy tuyến tính.
Hồi quy tuyến tính trong phân tích dự đoán
Trong phân tích dự đoán, hồi quy tuyến tính được sử dụng để xây dựng mô hình dự đoán giá trị của một biến mục tiêu dựa trên các biến độc lập. Mô hình hồi quy tuyến tính có thể được sử dụng để dự đoán giá cổ phiếu, doanh số bán hàng, giá nhà đất, v.v. Bằng cách lấy dữ liệu lịch sử và xây dựng một mô hình hồi quy, chúng ta có thể dự đoán giá trị của biến mục tiêu trong tương lai.
Ưu điểm của hồi quy tuyến tính trong phân tích dự đoán
- Dễ hiểu và giải thích: Mô hình hồi quy tuyến tính có cấu trúc đơn giản và dễ hiểu, giúp người dùng dễ dàng giải thích kết quả dự đoán.
- Hiệu suất tính toán cao: Thuật toán hồi quy tuyến tính có thể được tính toán một cách hiệu quả trên các tập dữ liệu lớn.
- Dự đoán chính xác: Khi các giả định của hồi quy tuyến tính được đáp ứng, mô hình có thể dự đoán chính xác giá trị của biến mục tiêu dựa trên các biến độc lập.
Nhược điểm của hồi quy tuyến tính trong phân tích dự đoán
- Giả định tuyến tính: Mô hình hồi quy tuyến tính giả định mối quan hệ giữa các biến là tuyến tính, điều này có thể không phản ánh đúng thực tế trong nhiều trường hợp.
- Nhạy cảm với dữ liệu nhiễu: Mô hình hồi quy tuyến tính có thể bị ảnh hưởng bởi dữ liệu nhiễu và outliers, dẫn đến kết quả dự đoán không chính xác.
- Không xử lý được dữ liệu không tuyến tính: Trong trường hợp mối quan hệ giữa các biến không phải là tuyến tính, mô hình hồi quy tuyến tính có thể không đưa ra kết quả chính xác.
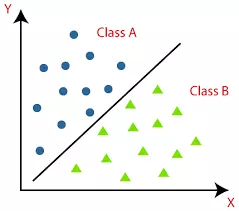
Hồi quy tuyến tính trong phân loại
Ngoài việc được sử dụng cho việc dự đoán giá trị số, hồi quy tuyến tính cũng có thể được áp dụng trong các bài toán phân loại dữ liệu. Trong trường hợp này, mô hình hồi quy tuyến tính được sử dụng để phân loại dữ liệu thành các nhóm khác nhau dựa trên ngưỡng quyết định (decision threshold). Bằng cách xác định ngưỡng phân loại phù hợp, mô hình hồi quy tuyến tính có thể được áp dụng trong các bài toán phân loại như phân loại email spam, phân loại khách hàng tiềm năng, v.v.
Ưu điểm của hồi quy tuyến tính trong phân loại
- Đơn giản và dễ hiểu: Mô hình hồi quy tuyến tính có cấu trúc đơn giản và dễ hiểu, giúp người dùng dễ dàng giải thích quyết định phân loại.
- Tính toán hiệu suất: Thuật toán hồi quy tuyến tính có thể được tính toán một cách hiệu quả, đặc biệt với các tập dữ liệu lớn.
- Khả năng giải thích: Hệ số hồi quy trong mô hình cung cấp thông tin về tầm quan trọng của các biến độc lập đối với quyết định phân loại.
Nhược điểm của hồi quy tuyến tính trong phân loại
- Giả định tuyến tính: Mô hình hồi quy tuyến tính giả định mối quan hệ giữa các biến là tuyến tính, điều này có thể không phản ánh đúng thực tế trong nhiều trường hợp phân loại phức tạp.
- Khó xử lý dữ liệu không tuyến tính: Trong trường hợp mối quan hệ giữa các biến không phải là tuyến tính, mô hình hồi quy tuyến tính có thể không đưa ra kết quả chính xác trong bài toán phân loại.
- Không xử lý được dữ liệu không cân bằng: Trong trường hợp dữ liệu phân loại không cân bằng, mô hình hồi quy tuyến tính có thể không đưa ra kết quả chính xác do sự thiên vị của mô hình.
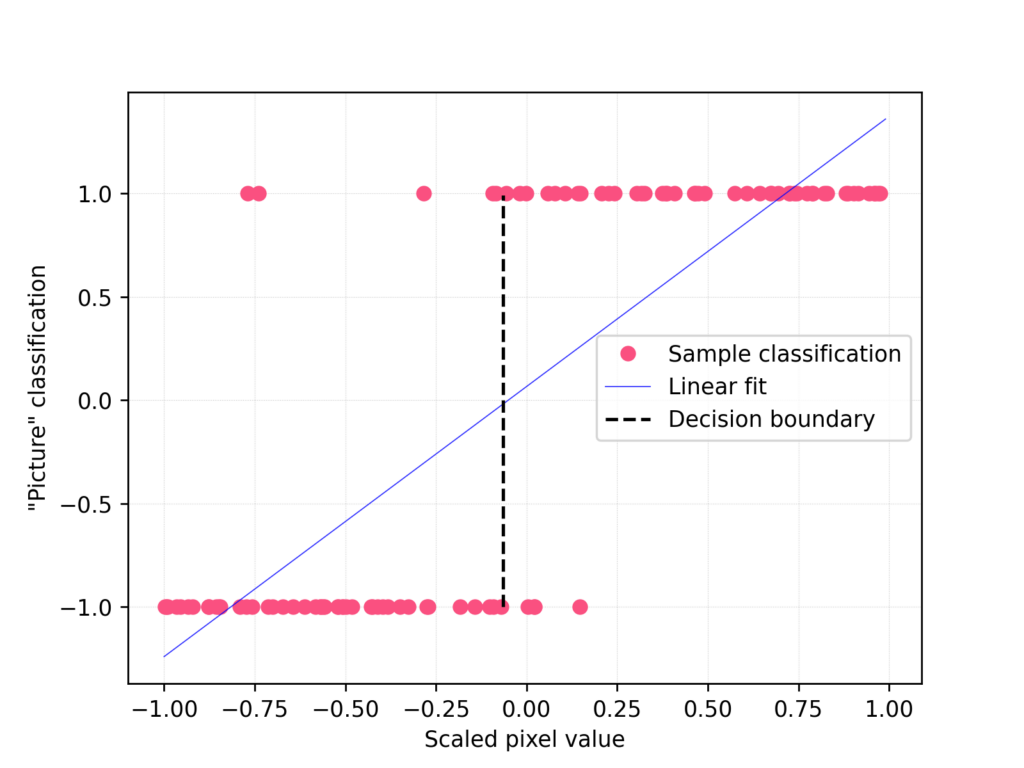
Hồi quy tuyến tính trong xử lý hình ảnh
Mặc dù hồi quy tuyến tính thường được sử dụng cho dữ liệu số, nó cũng có thể được áp dụng trong xử lý hình ảnh. Trong trường hợp này, các đặc trưng của hình ảnh được trích xuất và sử dụng làm biến độc lập trong mô hình hồi quy tuyến tính để dự đoán một biến mục tiêu, chẳng hạn như độ sáng, độ tương phản, v.v. Mô hình hồi quy tuyến tính có thể được sử dụng để điều chỉnh các thông số xử lý hình ảnh như cân bằng màu sắc, làm mịn hình ảnh, v.v.
Ưu điểm của hồi quy tuyến tính trong xử lý hình ảnh
- Đơn giản và linh hoạt: Mô hình hồi quy tuyến tính có cấu trúc đơn giản và linh hoạt, có thể được áp dụng cho việc điều chỉnh các thông số xử lý hình ảnh một cách dễ dàng.
- Dễ giải thích: Hệ số hồi quy trong mô hình cung cấp thông tin về tầm quan trọng của các đặc trưng hình ảnh đối với biến mục tiêu, giúp người dùng hiểu rõ quá trình dự đoán.
- Hiệu suất tính toán: Mô hình hồi quy tuyến tính có thể được tính toán một cách hiệu quả trên các tập dữ liệu hình ảnh lớn.
Nhược điểm của hồi quy tuyến tính trong xử lý hình ảnh
- Giả định tuyến tính: Mô hình hồi quy tuyến tính giả định mối quan hệ giữa các đặc trưng hình ảnh và biến mục tiêu là tuyến tính, điều này có thể không phản ánh đúng thực tế trong nhiều trường hợp xử lý hình ảnh phức tạp.
- Không xử lý được dữ liệu không tuyến tính: Trong trường hợp mối quan hệ giữa các đặc trưng hình ảnh không phải là tuyến tính, mô hình hồi quy tuyến tính có thể không đưa ra kết quả chính xác trong việc điều chỉnh các thông số xử lý hình ảnh.
Hồi quy tuyến tính trong phát hiện vật thể
Hồi quy tuyến tính cũng có thể được áp dụng trong phát hiện vật thể trong hình ảnh. Trong trường hợp này, các đặc trưng của vật thể được trích xuất và sử dụng làm biến độc lập trong mô hình hồi quy tuyến tính để dự đoán vị trí hoặc loại vật thể đó. Mô hình hồi quy tuyến tính có thể được sử dụng để phát hiện khuôn mặt, xe hơi, đồ vật, v.v., trong hình ảnh.

Ưu điểm của hồi quy tuyến tính trong phát hiện vật thể
- Đơn giản và linh hoạt: Mô hình hồi quy tuyến tính có cấu trúc đơn giản và linh hoạt, có thể được áp dụng cho việc phát hiện vật thể trong hình ảnh một cách dễ dàng.
- Dễ giải thích: Hệ số hồi quy trong mô hình cung cấp thông tin về tầm quan trọng của các đặc trưng vật thể đối với việc phát hiện, giúp người dùng hiểu rõ quá trình dự đoán.
- Hiệu suất tính toán: Mô hình hồi quy tuyến tính có thể được tính toán một cách hiệu quả trên các tập dữ liệu hình ảnh lớn.
Nhược điểm của hồi quy tuyến tính trong phát hiện vật thể
- Giả định tuyến tính: Mô hình hồi quy tuyến tính giả định mối quan hệ giữa các đặc trưng vật thể và biến mục tiêu là tuyến tính, điều này có thể không phản ánh đúng thực tế trong nhiều trường hợp phát hiện vật thể phức tạp.
- Không xử lý được dữ liệu không tuyến tính: Trong trường hợp mối quan hệ giữa các đặc trưng vật thể không phải là tuyến tính, mô hình hồi quy tuyến tính có thể không đưa ra kết quả chính xác trong việc phát hiện vật thể.
- Khả năng bị ảnh hưởng bởi nhiễu: Mô hình hồi quy tuyến tính có thể bị ảnh hưởng bởi nhiễu trong dữ liệu hình ảnh, dẫn đến việc dự đoán không chính xác vị trí hoặc loại vật thể.
Kết luận
Trong bài viết này, chúng ta đã tìm hiểu về hồi quy tuyến tính và ứng dụng của nó trong lĩnh vực học máy. Hồi quy tuyến tính là một phương pháp mạnh mẽ để dự đoán giá trị số và phân loại dữ liệu dựa trên mối quan hệ tuyến tính giữa các biến. Chúng ta đã thấy các phương pháp hồi quy tuyến tính khác nhau được áp dụng trong các bài toán phân tích dự đoán, phân loại, xử lý hình ảnh và phát hiện vật thể.
Mặc dù hồi quy tuyến tính có nhiều ưu điểm như đơn giản, dễ hiểu và tính toán hiệu suất, nhưng cũng tồn tại nhược điểm như giả định tuyến tính, khó xử lý dữ liệu không tuyến tính và không cân bằng. Để áp dụng hồi quy tuyến tính một cách hiệu quả, người sử dụng cần hiểu rõ về đặc điểm của dữ liệu và bài toán cụ thể để lựa chọn phương pháp phù hợp.
Tóm lại, hồi quy tuyến tính là một công cụ quan trọng trong học máy và có thể được áp dụng trong nhiều lĩnh vực khác nhau để giải quyết các bài toán phức tạp. Việc hiểu rõ về cách hoạt động và ứng dụng của hồi quy tuyến tính sẽ giúp cho việc xử lý dữ liệu và dự đoán trở nên chính xác và hiệu quả hơn.